Le proiezioni ortogonali sono un metodo di rappresentazione grafica che permette di rappresentare la realtà tridimensionale su piani di proiezione bidimensionali. Sembrano difficilissime, ma una volta capito il meccanismo tutto diventa più semplice.
Cerchiamo di capire che cosa sono, con un breve video del canale youtube Tecnologia Duepuntozero. Questo video in passato è stato inserito con mia grande soddisfazione su Rai Scuola 😵🤓
Se può esserti utile, scarica e stampa lo schema in formato pdf
Cosa sono le Proiezioni Ortogonali presentazione di Martina Baldini
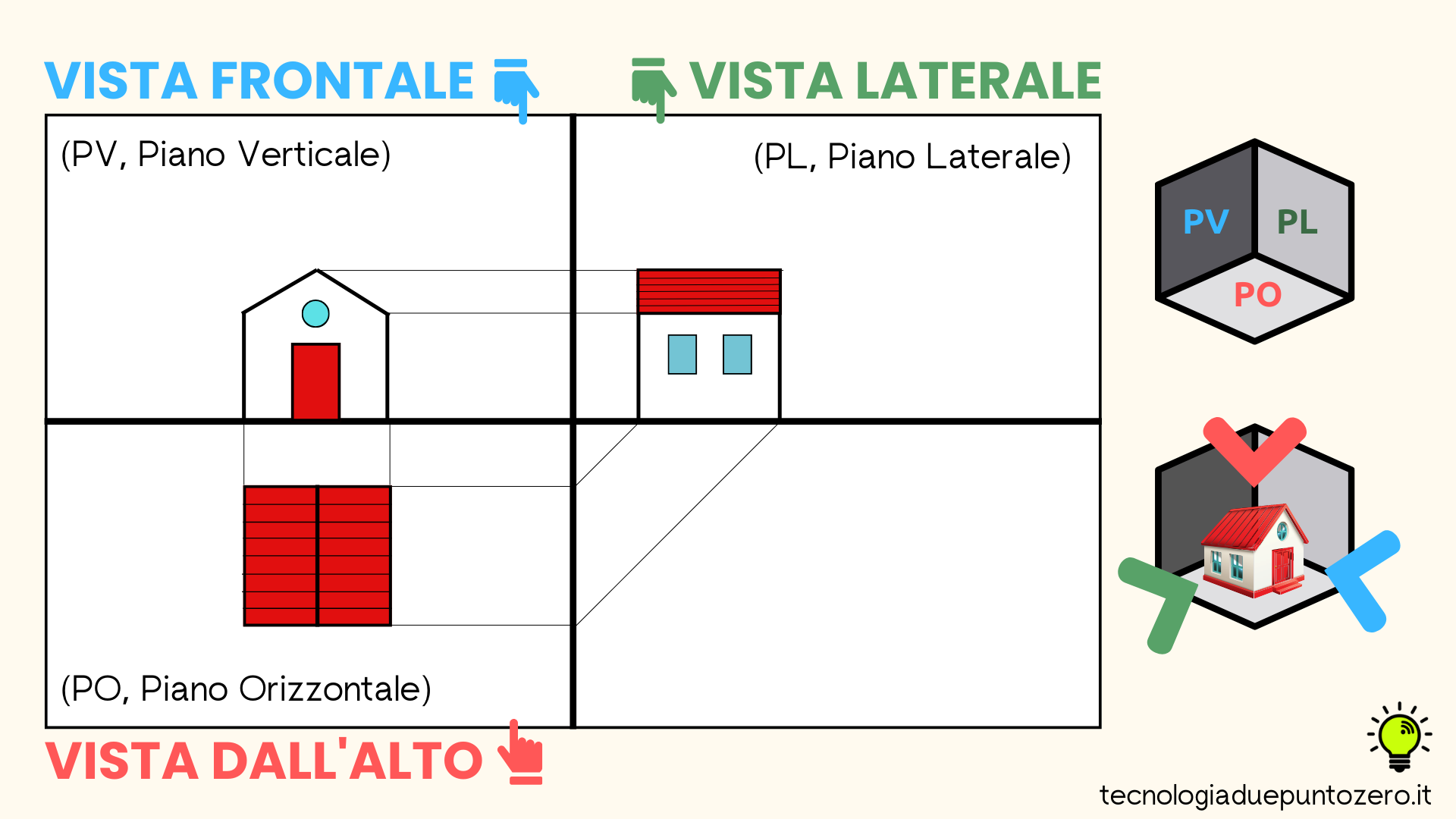
Le proiezioni ortogonali
Le proiezioni ortogonali sono una tecnica di rappresentazione grafica che permette di disegnare un oggetto tridimensionale da tre punti di vista diversi:
- la vista dall’alto (sul PO, piano orizzontale)
- la vista frontale (sul PV, piano verticale)
- la vista laterale (sul PL, piano laterale)
Questi tre piani di proiezione sono perpendicolari tra loro e formano il Triedro di Monge.
I raggi di proiezione sono paralleli tra loro e perpendicolari ai piani di proiezione.
Le proiezioni ortogonali permettono di rappresentare un oggetto tridimensionale su un foglio riportando in maniera precisa le forme, le dimensioni e i particolari dell’oggetto. Per questo motivo sono uno dei metodi di rappresentazione più usati dai disegnatori tecnici.
Tuttavia, le proiezioni ortogonali non permettono un’immediata visione d’insieme dell’oggetto, in quanto ne rappresentano tre punti di vista diversi.
Come nasce un disegno in proiezione ortogonale
Consideriamo un oggetto comune. Ad esempio, un tavolino. Immaginiamo di essere in una stanza vuota, con le pareti e il pavimento tra loro perpendicolari. Sistemiamo il tavolino parallelamente alle pareti.
Per rappresentare un oggetto con il metodo delle proiezioni ortogonali occorre per prima cosa osservare l’oggetto da punti di vista diversi.
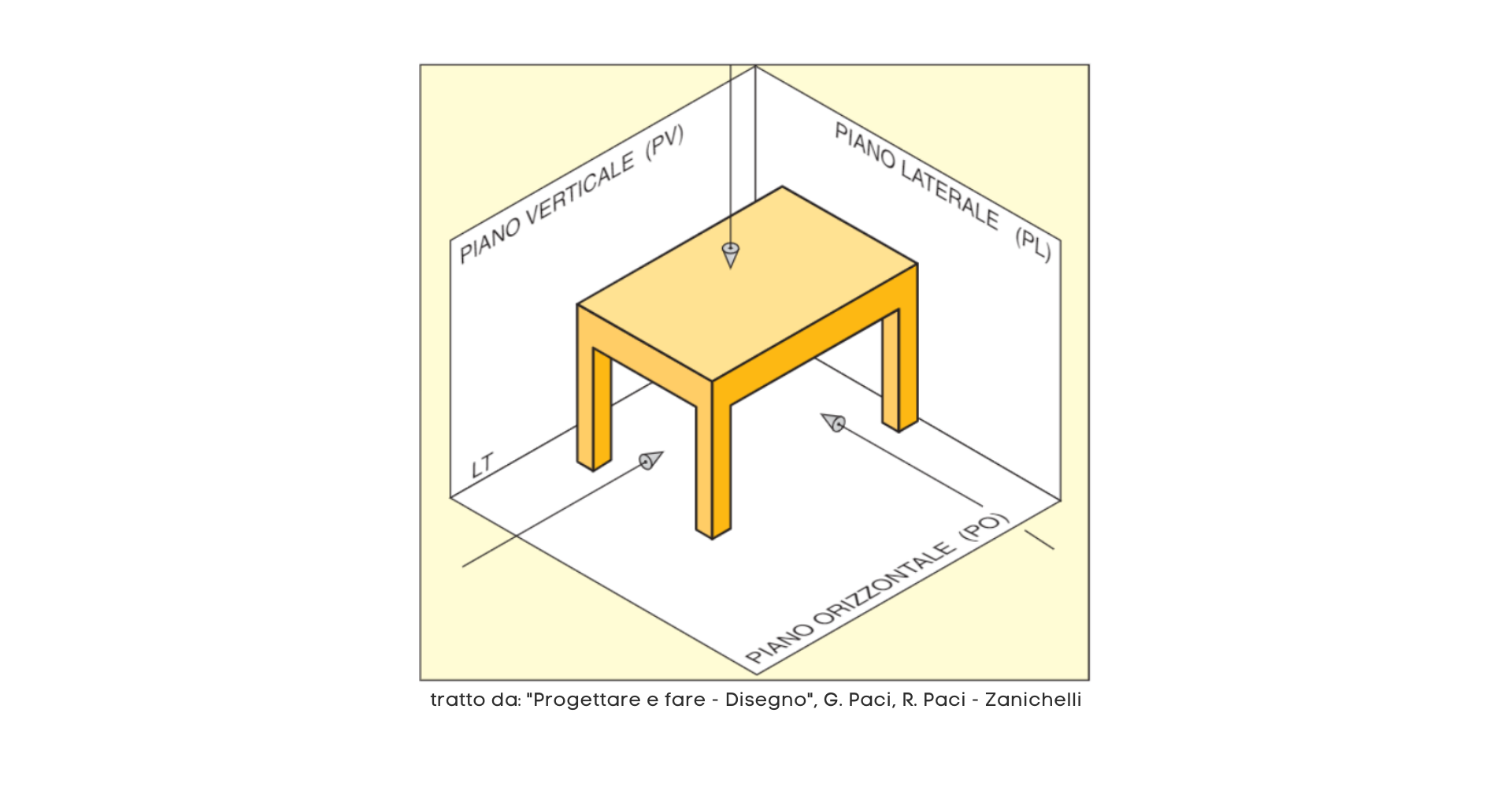
Le pareti saranno i nostri tre piani di proiezione, cioè i piani su cui proietteremo il tavolino. Le chiameremo Piano Orizzontale (PO), Piano Verticale (PV) e Piano Laterale (PL). Chiameremo invece linea di terra (LT) la linea che divide il pavimento dalle pareti.
Immaginiamo di girare intorno al tavolino per osservarlo da tre punti di vista ben precisi:
- vista di fronte (prospetto): da questo primo punto di vista vedremo il lato lungo del tavolino
- vista di lato (fianco): da questo primo punto di vista vedremo il lato corto del tavolino
- vista dall’alto (pianta): da questo primo punto di vista vedremo il piano del tavolino
Ogni volta vediamo solo una parte del tavolo. Immagino che il tavolino venga proiettato sui piani di proiezione che si trovano di fronte a noi attraverso raggi di proiezione ortogonali ai piani, come a farne tre foto.
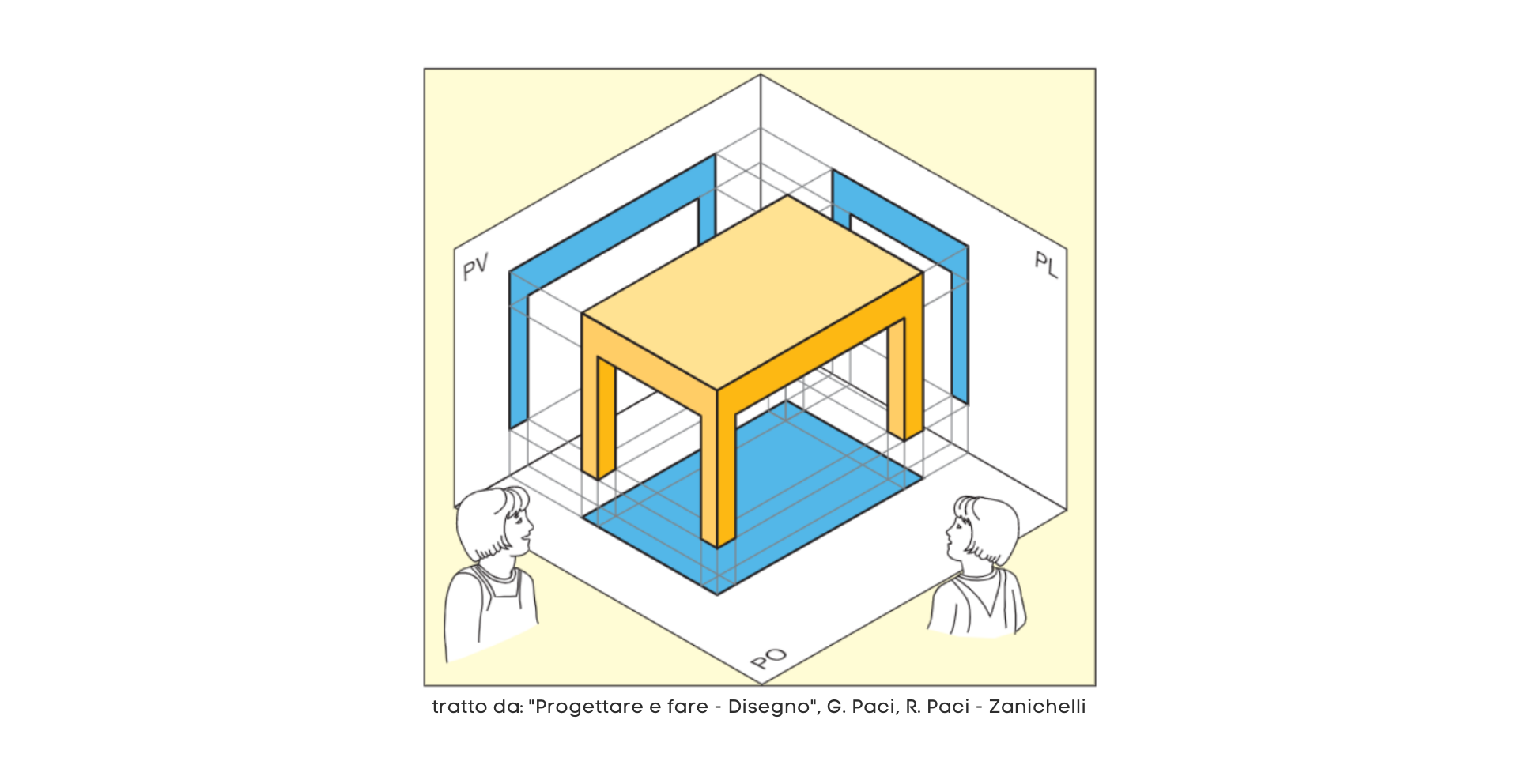
Il ribaltamento
Immaginiamo ora di togliere il tavolo dalla stanza, e che sulle pareti rimangano disegnate le tre proiezioni del tavolino: le tre viste. Immagino che le tre pareti siano tre fogli. Per riportarli tutti sullo stesso piano, dobbiamo ribaltare due piani (PL e PO), per allinearli con il terzo (PV)
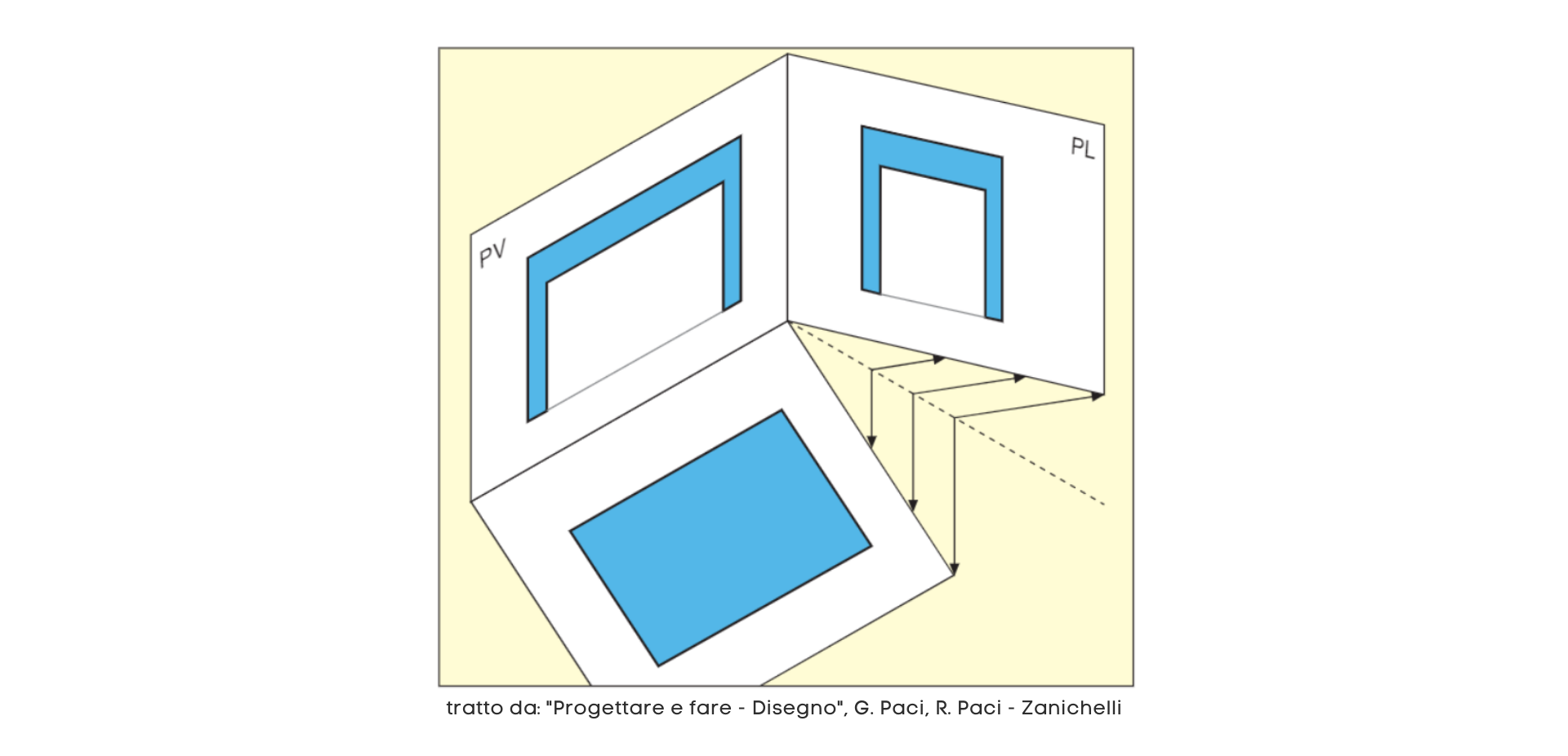
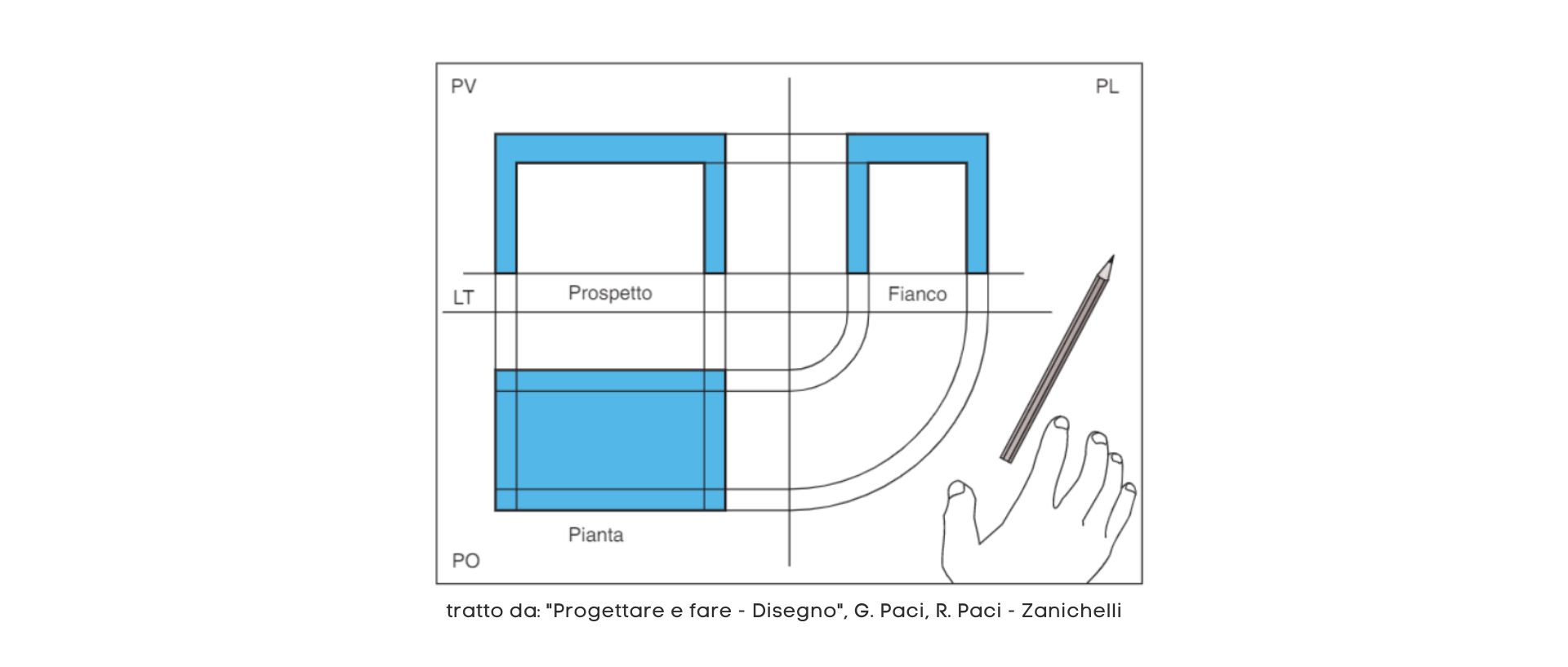
Tre viste su un piano
Ecco finalmente i tre disegni del tavolo sul foglio. Il foglio è diviso con due assi in quattro quadranti, tre dei quali sono il Piano Orizzontale (PO), il Piano Verticale (PV) e il Piano Laterale (PL). Su ognuno dei tre quadranti è disegnata una vista: il prospetto sul PV, il fianco sul PL e la pianta sul PO.
Di seguito, la Proiezione Ortogonale di una caffettiera (su gentile concessione della Prof.ssa Rossella Clausi)

Se può esserti utile, scarica la presentazione in formato pdf
Potrebbero interessarti anche:
Proiezioni ortogonali da completare… con Google Presentazioni
Proiezione Ortogonale di un cilindro con basi parallele a PV
Proiezione Ortogonale di un cilindro con basi parallele a PV
Proiezione Ortogonale di un prisma triangolare con base sul PO


