Artisti e scienziati si sono spesso misurati in un gioco che usa con malizia ingannatrice le regole delle tecniche di rappresentazione grafica. Il risultato è la creazione figure impossibili che possono generare sconcerto o disorientamento.
Guarda il video Inganni assonometrici del canale youtube Tecnologia Duepuntozero oppure leggi l’articolo sottostante
Inganni assonometrici
L’assonometria fornisce una rappresentazione bidimensionale (su foglio di carta) con forti suggestioni tridimensionali. Questo può indurci a interpretare in modo ambiguo alcune figure.
Questa figura può essere interpretata in chiave bidimensionale, come l’insieme di tre rombi, oppure, in ambito tridimensionale come un cubo o anche come un triedro formato da tre quadrati tra loro perpendicolari.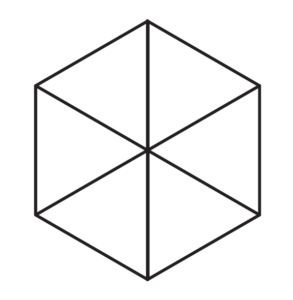
Questa figura rappresenta 6 triangoli oppure un cubo a fil di ferro, cioè con facce trasparenti? Se fosse un cubo, sarebbe visto dall’alto o dal basso?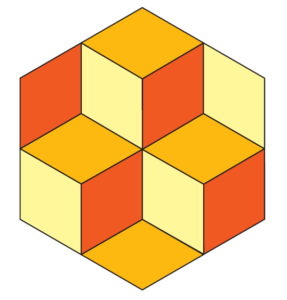
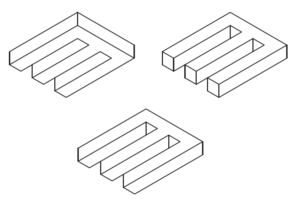
Questa figura rappresenta 12 rombi, oppure 3 cubi con 3 triedri?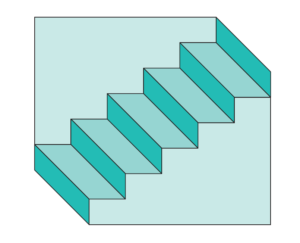
Questa scala è vista dall’alto o dal basso?
Inoltre, nel disegno assonometrico, se non si ha la massima chiarezza sulle caratteristiche dell’oggetto da rappresentare, è abbastanza facile commettere errori involontari: per esempio, scambiando le facce nascoste per facce visibili.
Qui abbiamo alcune rappresentazioni assonometriche di uno stesso solido. Il disegno di sinistra ha un’architettura concava: vediamo il solido rappresentato dal basso. Il disegno a destra, invece, ha un’architettura convessa, in cui si ha una visione dall’alto. Il disegno in basso è errato: si passa dall’architettura concava del lato sinistro a quella convessa del lato destro.
Talvolta le ambiguità delle rappresentazioni assonometriche vengono usate per ingannare la nostra percezione, creando figure impossibili che non trovano riscontro nella nostra esperienza percettiva. Artisti e scienziati si sono spesso misurati in un gioco che usa con malizia ingannatrice le regole delle tecniche di rappresentazione grafica. Il risultato è la creazione figure impossibili che possono generare sconcerto o disorientamento.
La litografia Concavo e convesso del fantasioso e geniale grafico Escher. Può essere suddivisa in tre strisce verticali: la striscia di sinistra ha un’architettura convessa, in cui si ha una visione dall’alto. Nella striscia di destra si vede tutto dal basso, e cioè si ha un’architettura concava. Nella fascia centrale, l’interpretazione è ambivalente. Il risultato è uno shock visivo. L’edificio ha una struttura simmetrica, eppure, una volta passata la zona centrale, sembra di precipitare in un abisso senza fondo: tutto viene invertito dall’interno all’esterno; il davanti diventa dietro, la parte superiore diventa parte inferiore.
Un parallelepipedo a fil di ferro può essere interpretato in modo ambiguo, a seconda di come si considerino disposti gli spigoli sovrapposti; se questi vengono dislocati in ordine inverso nei due punti di sovrapposizione, si genera una figura impossibile, come quella del celebre cubo di Necker.
Lo spunto fornito dallo studioso svizzero Necker è stato sfruttato da Escher nella sua litografia Belvedere. L’uomo seduto in basso maneggia un cubo di Necker e cerca di scioglierne l’enigma studiando con attenzione il disegno che c’è per terra davanti a lui. Pur avendo in mano gli elementi che potrebbero permettergli di notare che qualcosa non va, pare non accorgersi del fatto che l’intero Belvedere è progettato proprio su quella stessa struttura.
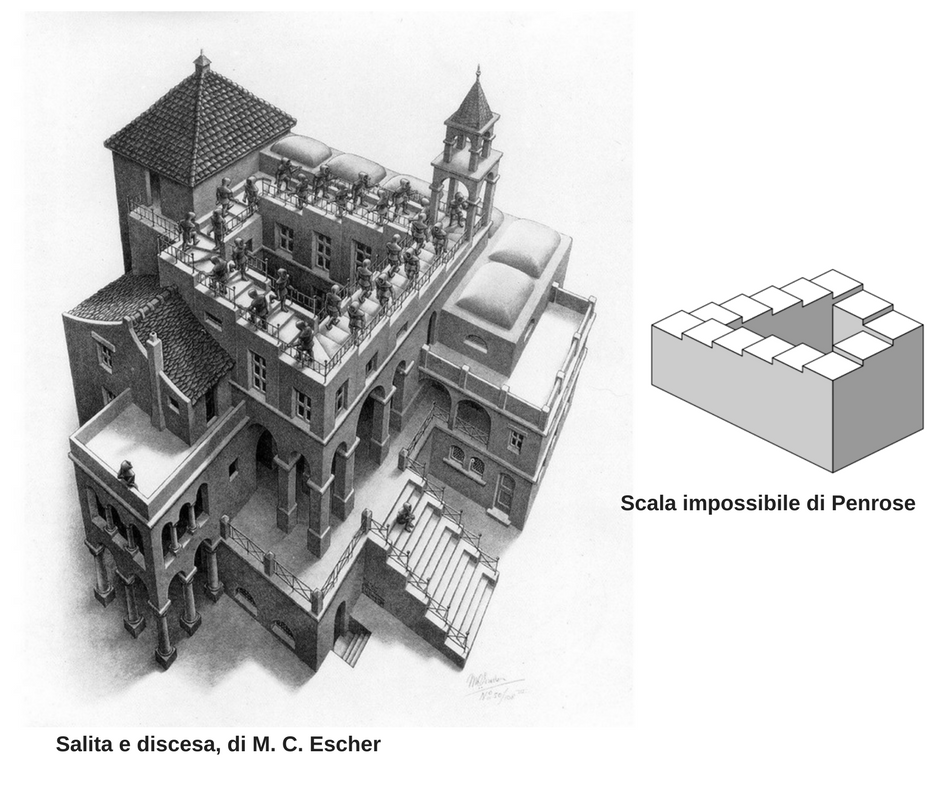
Successivamente, ispirato dal triangolo impossibile inventato dal matematico britannico Roger Penrose, ne illustrò l’assurdità con la litografia Cascata.
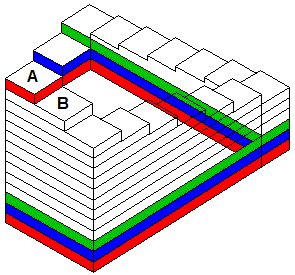
L’influenza che le opere di Penrose hanno avuto su Escher appare anche nella litografia Salita e discesa, nella quale si vedono alcuni monaci dediti a salire e scendere una scala che appare infinita, posta alla sommità di un monastero.
L’inganno si chiarisce se cerchiamo di evidenziare i vari livelli su cui si sviluppa la scala. Il liCome può una scala essere infinita, e portarci sempre allo stesso livello? Il livello su cui si trova lo scalino A in realtà è molto più basso di quello su cui si trova lo scalino B, anche se appare più alto.
La suggestione spaziale di un’immagine piana può essere così forte da suggerire mondi che, in tre dimensioni, non potrebbero assolutamente esistere.
Le illusioni ottiche possono essere utilizzate, per esempio, nel campo della sicurezza stradale. In alcune città dell’India e dell’Islanda sono state realizzate delle strisce pedonali che appaiono tridimensionali: guardandole, gli automobilisti hanno la sensazione che qualcosa stia bloccando la strada e d’istinto diminuiscono la velocità garantendo un attraversamento più sicuro ai pedoni.
Laboratorio
Costruiamo il modello del triangolo di Penrose
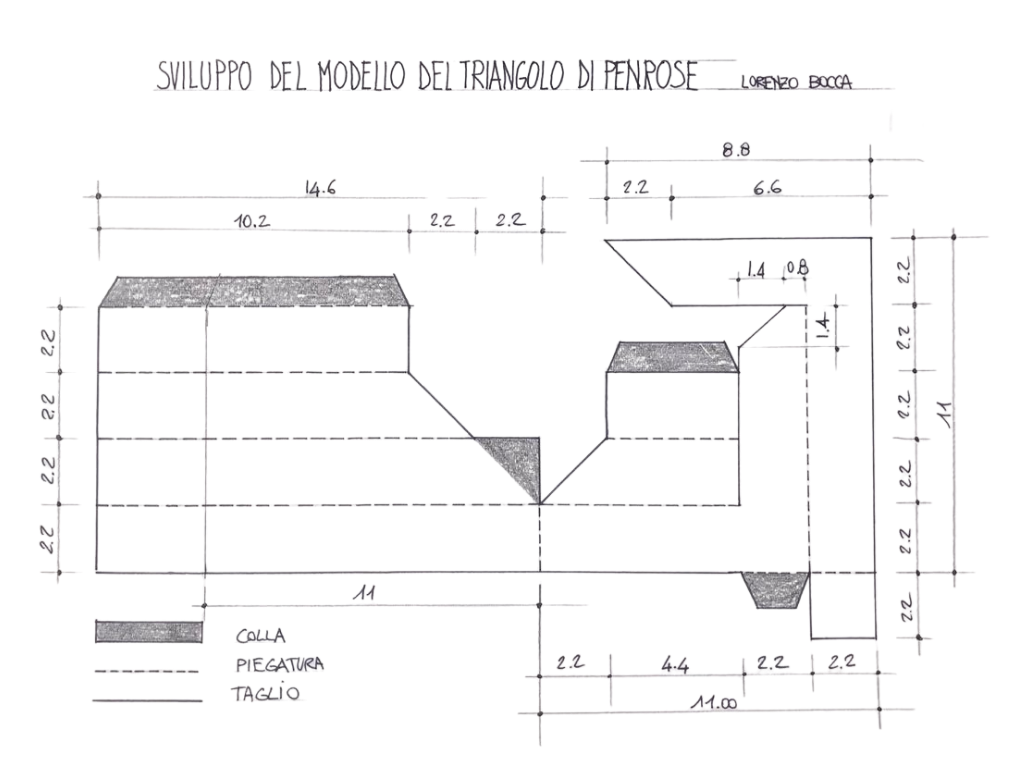
Tratto da:
“Lo specchio magico di M. C. Escher”, di Bruno Ernst, Evergreen
“Inganni assonometrici”, Sergio Sammarone, Zanichelli
Potrebbero interessarti anche: